Scikit-learn has a well designed, extensible implementation of decision trees. The design pays dividends for techniques that rely on decision trees such as random forest. Overall, the design is a great example of thoughtfully designed machine learning code and is worth learning from.

Before jumping into the design, lets first review what decision trees, random forests and extra trees are. If this is not new to you, jump ahead to Scikit-learn Design section.

What are Decision Trees

Decision trees are a machine learning technique which recursively splits a feature into two regions such that each region is easier to predict than the full data together. Splits are selected along a feature where a threshold determines the two regions. Datums with the feature value less than the threshold are in region and features with a value greater than the threshold are another region.

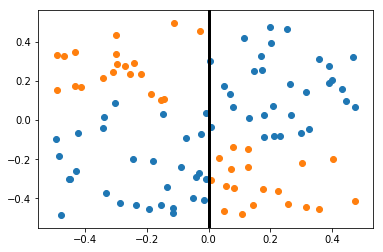For the problem of trying to classify the orange vs blue points, a split is made on the feature along the X axis at a threshold of 0. Subsequent splits will operate on the left and right regions recursively.

The algorithm can be viewed as a tree, where at each node the algorithm searches for a feature to split on and what the threshold for that feature should be. The feature and threshold selected will be the one that, if the split was made, would reduce a desired loss function the most.

The split produces two new nodes where datums with the feature below the threshold go to the left node and datums with the feature above the threshold go to the right node. For these two nodes, the algorithm repeats until a stopping condition is met. When the stopping condition is met, a leaf node is created which produces a prediction based on the datums in the leaf. For a regression problem a common choice is to use mean squared error for the loss function and predict the mean of the data in the leaf node.

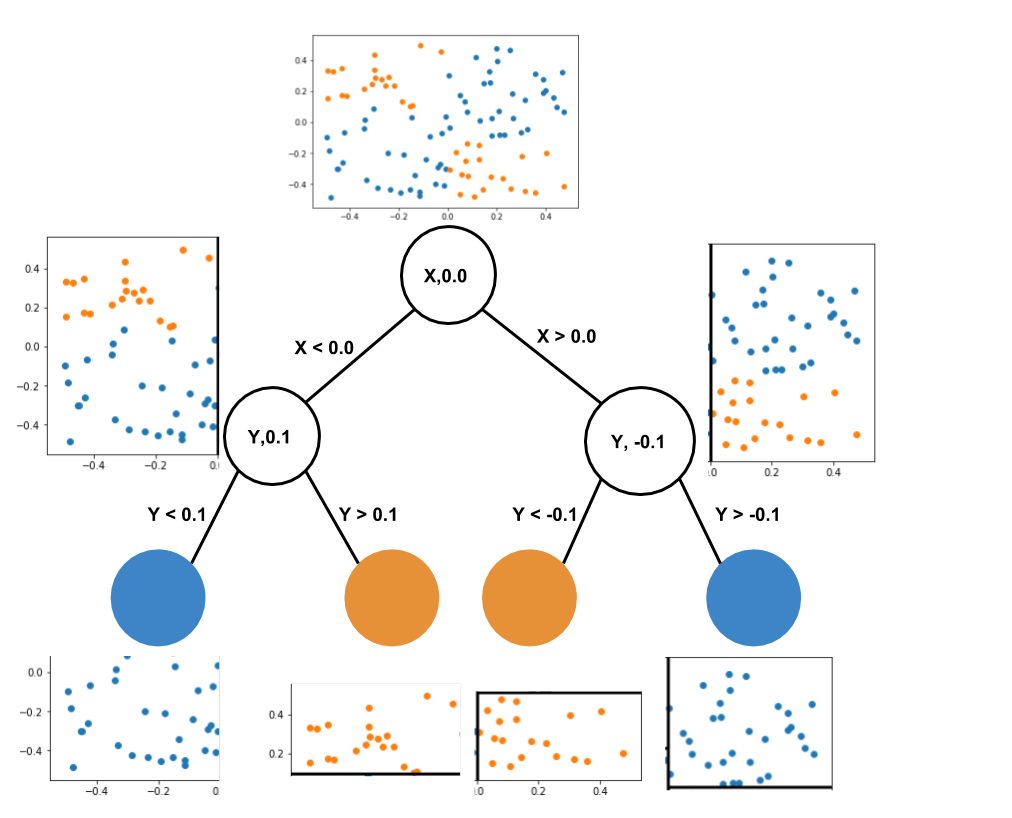The tree shows the feature and threshold it used for each split and how it recursively narrowed down the space to make more accurate predictions

Decision trees produce easily interpretable models. To predict a new datum, one may simply follow the splits down the tree to determine the prediction. Further, domain experts can inspect the splits to ensure they match intuition.

Unfortunately, decision trees don’t produce especially good models and their predictions have high variance because changing the initial training data slightly can result in a drastically different model.

Fortunately, the fact decision trees are high variance weak learners means they work especially well in an ensembling technique called bagging.

Bagging

Bagging is a technique which trains many weak learners on different bootstrapped samples of the original data and averages the weak learner’s predictions. Assuming the weak learners are uncorrelated, averaging their predictions reduces the variance of the overall predictions on the order of \(\frac{1}{sqrt(O(T))}\) where \(T\) is the number of trees. Even better, adding more weak learners won’t lead to overfitting.

Random Forest and extra trees are two techniques that use bagging with decision trees and differ only in how the trees search for splits.

Random Forests

Random forest searches for the best split at each node. This means it will try all possible (feature, threshold) split options and select the one that reduces the loss the most.

Extra Trees

Extra trees samples from the possible (feature, threshold) split options and selects the one that reduces the loss the most. This has the benefits of being faster to construct the trees and provides regularization while selecting splits.

Scikit-learn Design

The main class for Scikit-learns design is the DecisionTree. The DecisionTree extends BaseEstimator and is used by both RandomForest and ExtraTrees as the weak learner implementation. DecisionTree can be configured for either regression or classification, and search for the best split (to support RandomForest) or the best random split (to support ExtraTrees).

DecisionTree maintains the tree of nodes where each node encapsulates the feature and threshold used to split the node and prediction for the leaf nodes. While constructing the tree, DecisionTree relies on a component called a Splitter to search for the feature and threshold to split on. The Splitter uses a component called the Criterion to evaluate splits to find the split that best minimizes the impurity function associated with the given criterion. Both components are written in Cython because they can be called millions of times while fitting.

While at a high level the logic is the following, the design and implementation of the Splitter and Criterion allows for far great performance.

for feature, threshold in possible_splits:
    criterion.evaluate(feature, threshold)
return best_split

Design of the Splitter

The Splitter decides how to search for the feature and threshold to split the node on. Scikit-learn has two different splitters, BestSplitter and RandomSplitter. BestSplitter will search for the best possible split across features and threshold while RandomSplitter will sample features and threshold and select the best split of the ones sampled. BestSplitter is used by RandomForest and RandomSplitter is used by ExtraTrees.

A Splitter has a public function, node_split that produces a SplitRecord which encapsulates a feature and threshold. While the two splitters have different searching algorithms, they both maintain a list of features that are constant from ancestor nodes so they don’t need to check those features at each split descending down the tree. For each feature and threshold, the Splitter calls into the Criterion to first update the Criterion for the current split and then to produce a low cost proxy for the impurity of the split. Once the best split is selected, the Splitter resets the Criterion to the best split and computes the actual impurity for the split as well as the impurity for left and right children.

The psuedo-code is:

for feature in possible_features:
    for threshold, pos in possible_thresholds(feature):
        criterion.update(pos)
        criterion.proxy_impurity_improvement()
criterion.update(best_split.pos)
criterion.impurity_improvement()
return best_split

A lot of care is taken in the criterion to minimize computation so tree building is fast.

Design of the Criterion

The Criterion computes the impurity of a given split and produces the values the node will return for predictions. There are regression and classification specific Criterion that both fit within the same interface. It is critical that the Criterion is fast because it is called within the inner loop.

The Criterion was designed so that for a given feature, state can be maintained so that changing the split threshold from \(t_1\) to \(t_2\) requires computation on the order of the number of elements that moved from the right to the left child instead of the total number of elements in the node. This is crucial when using BestSplitter because BestSplitter will try all possible threshold values; recomputing the loss without state would be intolerably slow. As an example, the default regression Criterion, mse (mean squared error), maintains the count, sum and sum squared of the elements the left child and the total for the node so that changing the threshold requires adding or subtracting from the left child’s state and then computing the right child’s state requires subtracting the left child’s from the total’s.

The Criterion provides two functions to compute the impurity for a split; proxy_impurity_improvement and impurity_improvement. proxy_impurity_improvement is used while searching for the best split and implementations are able to drop any constant or proportional terms to reduce the cost of evaluating the split. When the best split is selected, impurity_improvement is called to get the correct value.

Finally, for leaf nodes, Criterion has a function, node_value, which returns the value the node predicts.

Scikit-learn provides mean squared error, mean absolute error, Friedman mean squared error as criterion for regression and gini and entropy for classification.

RandomForest and ExtraTrees

The extensibility of DecisionTree shows it true benefit when considering ensemble estimators that build off of DecisionTree; RandomForest and ExtraTrees.

RandomForest configures the splitter to be BestSplitter and allows the user to select the criterion desired. Similarly, ExtraTrees configures the splitter to be RandomSplitter and users may use the same criterion they selected for RandomForest.

Extending Scikit-learn Tree Design with new Criterion

While you can pass in a custom Criterion, extending the Criterion interface is difficult because Scikit-learn doesn’t provide the cython header file equivalent, .pxd files. In order to make them available, one most either implement the Criterion within the Scikit-learn package or manually copy the .pxd files to the proper Scikit-learn install directory so they can be imported.

Conclusion

Scikit-learn’s trees is an example of designing a general implementation that relies on composition allow for extending the tool for many applications.